[CS231n-Lecture 2] Image Classification

 

이미지 분류(Image Classification)는 컴퓨터 비전에서 매우 중요한 작업이지만, 컴퓨터에겐 매우 어려운 일이다.

이 강의에선 왜 이미지 분류가 어려운지, 데이터 중심 접근법인 NN과 K-NN 분류기는 무엇인지, 마지막으로 Linear classification대해 간략히 배울 수 있다.

---

[이미지분류 수행하는 방법]

이미지 입력 -> 컴퓨터는 미리 설정해 놓은 범주 또는 레이블 집합(개, 고양이, 트럭, 비행기 등) 매칭

⇒ 사람에게는 쉬운 문제처럼 보이지만 기계(컴퓨터)에겐 아주 어려운 문제 ⬇

---

1. semantic gap (의미론적 차이)

• 컴퓨터가 이미지를 볼 때 거대한 격자 모양의 숫자 집합으로 표현 (image pixels = height x width x channel)
• 각 픽셀은 Red, Green, Blue 값 제공하는 세 개의 숫자로 표현 (RGB)
• 의미상의 레이블 - "고양이", "강아지" 등

---

[우리의 알고리즘이 해결해야 할 문제]

 

2. Challenges

1) Viewpoint variation - 이미지에 아주 작고 미묘한 변화가 생기더라도 픽셀 격자가 완전히 변경됨 2) Illumination - 빛, 조명에 따라서 이미지 픽셀 값은 영향 받음 3) Deformation - 객체 변형에 의해 다르게 보일 수 있음

4) Occlusion - 형체 일부만 볼 수 있는 교합 문제(가려짐) 5) Background clustter - 실제로 배경과 객체가 매우 유사 하게 보여 구분을 할 수 없음 6) Intraclass variation - 하나의 클래스 내 다양한 특징 존재

---

3. Data-Driven Approach - 데이터 중심 접근법

• 인터넷을 통해 많은 대규모 이미지 데이터 수집함 (고양이, 비행기, 사슴 다른 것들..)
• 머신 러닝(ML)사용하여 분류 학습
• 새 이미지를 학습 시킨 모델에 넣어 성능 테스트 (분류기 평가)

 

⬇ 입력 이미지 인식하기 위해 2개 함수 필요

Train 함수 (입력 : images, labels / 출력 : model)

Predict 함수 (입력 : model, test_images / 출력 : test_labels) = 이미지 예측 값

 

---

4. Nearest Neighbor(NN)

: 가장 단순한 분류기(classifier)

학습 단계(train step)에서 모든 학습 데이터 기억해 모델로 만든 후,

예측 단계(predict step)에서 새로운 이미지가 들어왔을 때 기존의 학습 데이터를 비교해 가장 유사한 이미지 찾고 이미지의 레이블을 예측함(L1 Distance 사용)

 

⇒ NN classifier 실제 적용하여 결정 영역을 그렸을 때, 학습은 매우 빠르나

녹색 점 사이 노란 점이 끼거나, 녹색 영역이 파란 영역을 침범하는 문제 발생 (nosie or spurious)

 

• 가까운 이웃만 찾기 때문에 분류가 제대로 되지 않으면 좋지 X

 

---

5. K-Nearest Neighbor(K-NN)

: NN의 일반화된 버전.

• 가장 가까운 이웃만 찾는 것이 아니라 distance metric 이용해서 가까운 이웃을 K개 만큼 찾고, 이웃끼리 투표해 가장 많은 득표수(과반수) 를 획득한 레이블로 예측하는 방법

⇒ K=3, K=5 결과 모두 중앙에 노란색이 표시 되지 않고, 녹색 부분이 모두 녹색으로 분류, 빨강색과 파랑색 영역 사이의 결정 경계가 아주 매끄럽게 좋아짐

• K=1 보다 커야 결정 경계 부드러워지고 더 좋은 결과 가져옴
• 거리 척도만 정해주면 다양한 데이터 다룰 수 있음
• 흰색영역 임의로 정할 수 있음 (=가장 가까운 이웃이 없음)

---

6. Distance Metric

 

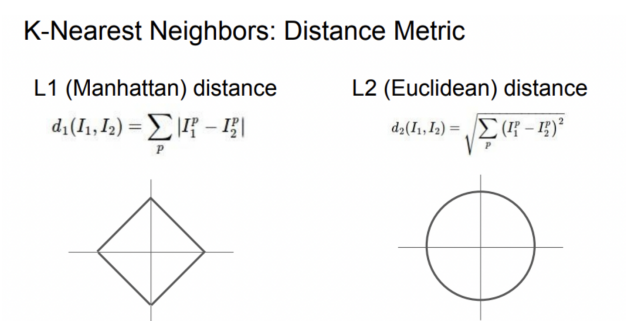
L1 - Manhattan distance (맨하탄거리)	L2 - Edclidean distance (유클리드 거리)
- 픽셀 차이 절대값의 합을 이용 - 이미지를 Pixel-wise로 비교 - 선택한 좌표에 따라 달라짐(영향받음)	- 제곱 합의 제곱근을 거리로 이용 - 두 점간의 최단 거리 - 좌표계와 관련없음

특징 벡터의 각각 입력값 요소들이 개별적인 의미를 가지고 있다면 (개별요소) -> L1

특징 벡터가 일반적인 벡터이고, 요소들 간의 실질적인 의미 잘 모르는 경우 -> L2

---

Q. L1/L2 무엇을 사용할 것인지 ❓ ❓

 

7. Hyperparameters

훈련 데이터에서 반드시 학습되는 것은 아니기 때문 학습 전에 반드시 선택.

데이터와 다양한 하이퍼파라미터의 다른 값을 시도해보고 그 중 최고(가장 잘 작동하는지)를 알아내야함.

 

 

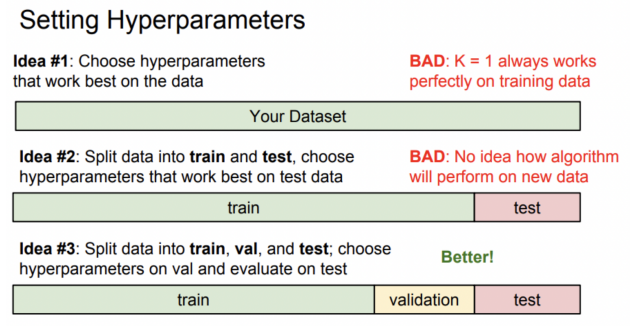
① 학습데이터에서 최고의 정확도 or 최고의 성능을 제공하는 하이퍼파라미터 선택 (ebs)  => BAD ❌

② 전체 데이터 셋을 가져와서 일부 훈련 데이터 / 테스트 데이터로 나눔 => BAD ❌

③ 일반적인 방법 : 데이터를 세개로 나눔 => Better !

ㄴ 대부분은 training set, 일부는 validation set(검증 셋), 나머지 test set

=> 다양한 하이퍼파라미터로 training set 학습 -> validation set 검증 후 가장 좋은 하이퍼파라 미터 선택 -> 가장 좋은 분류기 가지고 test set 한번 수행

 

④ cross validation(교차 검증)

우선 test set 정해둠(마지막에만 사용) -> 나머지 데이터는 traing/validation set으로 나눠줌 (데이터를 여러부분으로 나눠 5겹 교차 검증 사용 번갈아 가면서 validation set 지정)

→ 딥러닝에서 대규모 모델을 훈련하고 훈련에 계산 비용이 매우 많이 드는 경우, 실제로 많이 사용 X, 작은 데이터셋 많이 사용

 

=> 실제로 입력값이 이미지인 경우  k-NN classifier 잘 사용하지 않는다.

 

---

 

① 테스트 시간 매우 느리다.

② L1/ L2 거리와 같은 거리 측정법들이 실제로 이미지 간의 거리를 측정하는 좋은 방법이 아니다.

: 3개(Boxed, Shifted, Tinted)의 사진들은 original과 모두 동일한 L2 거리에 있지만 서로가 확 연히 다르다.

 

③ 차원의 저주

: k-NN classifier 잘 작동하려면, 공간을 조밀하게 다루기 위해 충분한 훈련 예제가 필요 (많은 트레이닝 샘플 필요)

고차원의 이미지는 k-NN으로 공간을 잘 분할할 만큼의 데이터를 모으는 일이 현실적으로 불가능함.

 

---

<요약>
In Image classification we start with a training set of images and labels, and must predict labels on the test set
이미지 분류에서는 우리는 이미지와 라벨의 training set로 시작하고, test set 라벨을 예측 해야한다.
The K-Nearest Neighbors classifier predicts labels based on nearest training examples
K-NN classifier는 가장 가까운 트레이닝 예제를 기반으로 레이블을 예측한다.
Distance metric and K are hyperparameters
거리 측정과 K는 하이퍼파라미터이다.
Choose hyperparameters using the validation set; only run on the test set once at the very end !
validation set을 사용하여 하이퍼파라미터를 선택; 맨 마지막 test set에서 한 번 실행한다.

---

8. Linear Classification

• linear classifier. Deep learning 자주 사용
• NN, CNN 기반 알고리즘으로 매우 중요
• Parametric model의 가장 단순한 형태

 

f(x,W)=Wx+b

x : 입력 이미지

W : 파라미터(매개변수) 또는 가중치

b : 편향(bias)

 

예)

2x2 이미지(간단한 이미지) => 4개의 요소가 있는 열 벡터로 확장

cat, dog, ship 3개의 클래스로 제한

가중치 행렬 4x3 (4개의 픽셀과 3개의 클래스)

각 범주에 대한 데이터 독립 편향 항을 제공하는 3요소 편향 벡터(bias term)

행렬의 행과 이미지의 픽셀을 제공하는 열벡터 간의 내적을 계산

내적 종류를 계산하면 클래스에 대한 이 템플릿과 이미지 픽셀 간에 유사성 얻음

bias는 다시 각 클래스에 대해 scaling offset을 더해줌

 

 

Linear classifier는 단순히 행렬과 벡터 곱의 형태이고, 템플릿 매칭과 관련이 있으며

각 카테고리에 대해 하나의 템플릿을 학습한다.